Unidad 3
CONJUNTO DE LOS NÚMEROS
NÚMEROS REALES
Son los que abarcan a los números racionales y los números irracionales. Se los representan con la letra R
NÚMEROS RACIONALES
Es una cifra o valor que puede ser referido como el cociente de dos números enteros o más.
NÚMEROS IRRACIONALES
Un número irracional si posee infinitas cifras decimales no periódicas.
NÚMEROS NATURALES
Son los números con los que contamos los elementos de un conjunto, o expresamos el orden o la posición que ocupa un elemento en un conjunto.
NÚMEROS ENTEROS
El conjunto de los números enteros está formado por los naturales, sus opuestos y el cero.
RECTA NUMÉRICA
Es la representación gráfica de los números Enteros
NÚMEROS PRIMOS
Son aquellos que solo son divisibles entre ellos mismos y la unidad.
NÚMEROS COMPUESTOS
Son aquellos números que además de ser divisibles por ellos mismos y la unidad, también son divisibles por otros números.
MÍNIMO COMÚN MÚLTIPLO (m.c.m)
Es el menor entero positivo que es el múltiplo de cada uno de los números dados
MÁXIMO COMÚN DIVISOR (M.C.D)
Es el mayor entero positivo que es divisor de cada uno de los números del conjunto.
REPRESENTACIÓN EN LA RECTA NUMÉRICA
NOTA: En una fracción el denominador no no puede ser 0
OPERACIONES ENTRE NÚMEROS REALES
ADICIÓN.-
Sean a y b números reales, entonces la adición o suma de estos números se le denota como a+b y cumple con las siguientes propiedades:
- a+b=b+a. La suma Conmutativa
- a+(b+c)=(a+b)+c. La suma es Asociativa
- a+0=a. Donde 0 es llamado Idéntico Aditivo
- a+(-a)=0. Donde -a es llamado Inverso Aditivo de a
RESTA
Se la considera como una suma de a con el inverso aditivo de , es decir: a +(-b)
MULTIPLICACIÓN
Sean a y b números reales, entonces la multiplicación de estos números se la denota como a*b y cu,ple con las siguientes propiedades:
- a*b=b*a. La multiplicación es Conmutativa
- a*(b*c)=(a*b)*c. Lamultiplicación es Asociativa
- a*1=a. Donde 14 es llamado Idéntico Multiplicativo
- a*(1/a)=1. Donde 1/a es llamado Inverso Multiplicativo de a*a(a≠0)
DIVISIÓN
Se la considera como una multiplicación al inverso
OPERACIONES COMBINADAS
Para resolver las operaciones combinadas se realiza lo siguiente:
- Efectuar las operaciones entre paréntesis del más interno al más externo
- Desarrollar potencias de raíces
- Desarrollar multiplicación y división de izquierda a derecha
- Desarrollar las sumas y las restas de izquierda a derecha
Ejemplo:
40/5+8²*3
40/5+64*3
8+64*3
8+192
200
EJERCICIOS
En este ejemplo, tenemos paréntesis. Por tanto, tenemos que resolver las operaciones que hay dentro de ellos. ¡Cuidado! Dentro de los paréntesis hay varias operaciones, por eso tenemos que fijarnos en hacer primero las multiplicaciones y divisiones dentro de los paréntesis:

Una vez que tengamos presente qué operaciones son las que tenemos que resolver primero, podemos calcularlas:

Ahora, como dentro de los paréntesis hay solo una operación podemos resolverlos:

Una vez quitados los paréntesis volvemos a fijarnos en las operaciones. Primero hay que hacer la multiplicación:

Una vez resuelta la multiplicación podemos resolver la expresión:

NÚMEROS DECIMALES
TIPOS DE NÚMEROS DECIMALES
- Decimales Finitos (0,25; 2,4)
- Decimales Infinitos Periódicos (0,333....)
- Decimales Infinitos Semiperiódicos (2,1666...)
TRANSFORMACIÓN DE NÚMEROS DECIMALES
DECIMALES FINITOS
Se caracteriza por tener una cantidad finita de dígitos después de la coma decimal, hacia la derecha.
DECIMALES INFINITOS PERIÓDICOS
Se caracterizan por tener uno o más dígitos que se repiten infinitamente en el mismo orden, inmediatamente después de la coma decimal hacia la derecha. La cifra que se repite se llama periodo.
DECIMALES INFINITOS SEMIPERIÓDICOS
Se caracterizan por tener una o más cifras ates del periodo, que forman lo que denomina el anteperiodo
EXPRESIONES ALGEBRAICAS
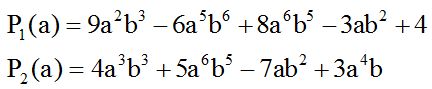
Ordenamos y completamos:
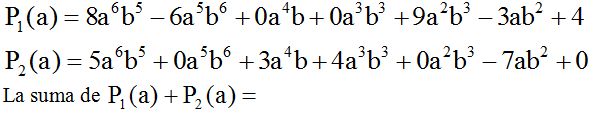
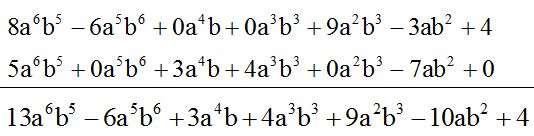
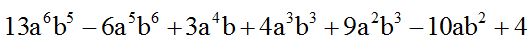
Es una expresión en la que se relacionan valores indeterminados con constantes y cifras, todas ellas ligadas por un número finito de operaciones de suma, resta, producto, cociente, potencia y raíz.
Ejemplo
a) x²+2xy
EXPRESIONES ALGEBRAICAS COMUNES
- El doble o duplo de un número : 2x
- El triple de un número: 3x
- El cuadrúplo de un número : 4x
- La mitad de un número x/2
Sumar los polinomios:
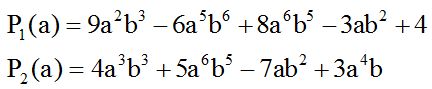
Solución:
Ordenamos y completamos:
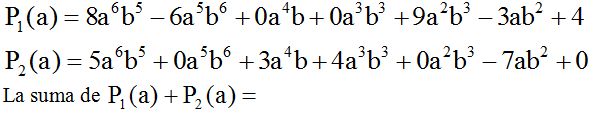
Es igual a:
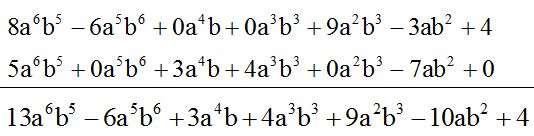
Respuesta:
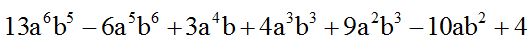
RAZONES Y PROPORCIONES
RAZÓN
Es una comparación entre dos cantidades, a y b.
Se representa:
Los demógrafos que estudian la evolución de las poblaciones, utilizan la razón para establecer natalidad anual
PROPORCIÓN
Es una igualdad de dos razones equivalentes. Se representa de la siguiente manera:
A:B=C:D ó A/B=C/D
PROPORCIÓN DIRECTA
Es cuando al aumenta una magnitud también aumenta la otra; o cuando disminuye la una , la otra también lo hace.
PROPORCIÓN INVERSA
Es cuando al aumentar el alor de una magnitud, disminuye la otra, o viceversa.
PROPORCIÓN COMPUESTA
Son las que tienen más de dos magnitudes
VALOR ABSOLUTO
ECUACIONES E IGUALDADES
El valor absoluto de un número consiste en su valor, sin importar su signo.
El valor absoluto puede ser explorado ya sea numérica o gráficamente. Numéricamente, el valor absoluto se indica encerrando el número, variable o expresión dentro de barras verticales, así:
|20|
|x|
|4n − 9|
Cuando tomamos el valor absoluto de un número, éste es siempre positivo o cero. Si el valor original ya es positivo o cero, el valor absoluto es el mismo. Si el valor original es negativo, simplemente nos deshacemos del signo. Por ejemplo, el valor absoluto de 5 es 5. El valor absoluto de -5 es también 5.
Ejemplo
| |
Valor
|
Valor
Absoluto
|
5
|
5
|
-5
|
5
|
IGUALDAD
Es aquella que se compone de dos expresiones numéricas unidas por el signo igual.
ECUACIÓN
Es aquella que contiene en sus miembros incógnitas. También se puede llamar igualdad algebraica
.Ejemplo:
x+10=20-12
PASOS PARA RESOLVER ECUACIONES DE PRIMER GRADO
- Quitar paréntesis
- Suprimir de ambos términos los miembros iguales
- Pasar a un miembro los términos que contengas la incógnita, y al otro miembro los números
- Reducir términos semejantes
- Despejar la incógnita
Es de la forma ax²+bx+c=0
ECUACIÓN CUADRÁTICA INCOMPLETA
- Cuando b=0
- Cuando c=0
ECUACIÓN CUADRÁTICA COMPLETA
ECUACIÓN CON TRINOMIO CUADRADO PERFECTO
x²+4x+4=0
(x+2)²=0
DISCRIMINANTE
Se llama discriminante de una ecuación de segundo grado de valor:
Δ=b²-4ac
El nº de soluciones de una ecuación de segundo grado de penderá del signo del determinante
Δ>0➡Tiene 2 soluciones reales distintas
Δ=0➡Tiene 1 solución DOBLE
Δ<0➡No tiene solución
INECUACIONES
Una inecuación es una desigualdad algebraica en la que sus dos miembros aparecen ligados por uno de estos signos:
| < | menor que | 2x − 1 < 7 |
| ≤ | menor o igual que | 2x − 1 ≤ 7 |
| > | mayor que | 2x − 1 > 7 |
| ≥ | mayor o igual que | 2x − 1 ≥ 7 |
La solución de una inecuación es el conjunto de valores de la variable que verifica la inecuacíón.
Podemos expresar la solución de la inecuación mediante:
1. Una representación gráfica.
2. Un intervalo.
Ejemplos
2x < 8 x < 4

(-∞, 4)
2. 2x − 1 ≤ 7
2x ≤ 8 x ≤ 4

(-∞, 4]
3. 2x − 1 > 7
2x > 8 x > 4

(4, ∞)
4. 2x − 1 ≥ 7
2x ≥ 8 x ≥ 4

[4, ∞)
RESOLVER LAS SIGUIENTES INECUACIONES



SUCESIONES
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
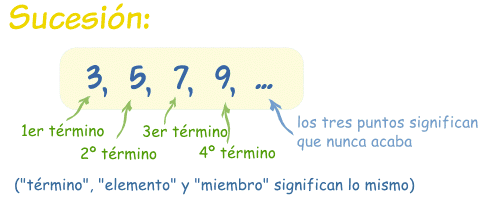 |
Finita o infinita
Si la sucesión sigue para siempre, es una sucesión infinita,
si no es una sucesión finita
si no es una sucesión finita
Notación
Para que sea más fácil escribir las reglas, normalmente lo hacemos así:
- xn es el término
- n es la posición de ese término
xn = 2n+1
Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
Sucesiones aritméticas
El ejemplo que acabamos de usar, {3,5,7,9,...}, es una sucesión aritmética (o progresión aritmética), porque la diferencia entre un término y el siguiente es una constante.
Ejemplos
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
Esta sucesión tiene una diferencia de 3 entre cada dos términos.
La regla es xn = 3n-2
La regla es xn = 3n-2
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
Esta sucesión tiene una diferencia de 5 entre cada dos términos.
La regla es xn = 5n-2
La regla es xn = 5n-2
Sucesiones geométricas
En una sucesión geométrica cada término se calcula multiplicando el anterior por un número fijo.
Ejemplos:
| 2, 4, 8, 16, 32, 64, 128, 256, ... |
Esta sucesión tiene un factor 2 entre cada dos términos.
La regla es xn = 2n
La regla es xn = 2n
| 3, 9, 27, 81, 243, 729, 2187, ... |
Esta sucesión tiene un factor 3 entre cada dos términos.
La regla es xn = 3n
La regla es xn = 3n
| 4, 2, 1, 0.5, 0.25, ... |
Esta sucesión tiene un factor 0.5 (un medio) entre cada dos términos.
La regla es xn = 4 × 2-n
La regla es xn = 4 × 2-n











Comentarios
Publicar un comentario