Unidad 2

CONJUNTOS

Conjunto es la agrupación de elementos que tengan una característica en común.

Los objetos que constituyen un conjunto se les llama miembros o elementos del conjunto.

Hay que tener en cuenta que:

• Todo conjunto se escribe entre llaves { }
• Se denota mediante letras mayúsculas 
• Sus elementos se separan mediante coma (,); (;)

EJEMPLOS: 

A= {1,3,5,7}

B= {x/x² -3x-2=0}        

C= {Inglaterra, Francia, Dinamarca}

RELACIÓN DE PERTENENCIA

Sirve para indicar si el elemento pertenece o no a un conjunto. El símbolo de pertenencia es ∈ y su negado es ∉

DETERMINACIÓN DE UN CONJUNTO 

Las formas de determinar un conjunto son:

• Por Extensión 
• Por Comprensión
• Diagrama de Venn

POR EXTENSIÓN O TABULACIÓN.- Es cuando se lista todos los elementos del conjunto. Ejemplo:

El conjunto de los números pares mayores que que 7 y menores que 21

A={ 6,8,10,12,14,16,18,20}

POR COMPRENSIÓN.- Cuando se escribe la característica del conjunto. Ejemplo:

A={1,3,5,7,9}

B={x/x ∈ a los números impares x>0 ^ x ≤ 9}

DIAGRAMAS DE VENN.- Conocido así por el filósofo inglés John Venn (1834 - 1883). Es la representación Gráfica de un conjunto.

CARDINALIDAD DE UN CONJUNTO 

Sirve para encontrar la cantidad de elementos de un conjunto A. Se simboliza por N(A). Ejemplo:

A={ a,b,c,d,e}      su cardinalidad N(A)=5

NOTA: No se contarán los elementos repetidos, sólo valdrá por uno mismo.

EJERCICIOS:

Dado el conjunto calcular la cardinalidad

A={1,4,7,10,........,22}

B={2,4,6,.........,26}

N(A)= 8

N(B)= 13

N(A)+N(B)= 21

Ver más ejercicios de Conjunto; tipos de conjunto y Cardinalidad.

TIPOS DE CONJUNTOS 

• Conjunto Vacío
• Conjunto Unitario
• Conjunto Finito
• Conjunto Infinito 
• Conjunto Universo o Referencial

CONJUNTO VACÍO.- Es un conjunto que no tiene elementos. Se lo representa por {}, ø

Ejemplos:

A={ números mayores que 9 y menores que 5}

B={ x/x es un número par e impar a la vez}

CONJUNTO UNITARIO.- Es el conjunto que tiene un único elemento. 

Ejemplo:

A={ x/x son las vocales que pertenecen ala palabra vals}

CONJUNTO FINITO.- Es el conjunto con un limitado número de elementos.

Ejemplo:

A={x/x días de la semana}

CONJUNTO INFINITO.- Es el conjunto ilimitado de elementos. 

Ejemplos:

A={1,2,3,4,.......}

B={x/x <6}

CONJUNTO UNIVERSO.- Es el que contiene todos los elementos que deseen considerarse en un problema, discurso o tema, sin pretender contener todo lo que no interesa al problema.

Ejemplo:

A={x/x es una letra del alfabeto español}

SUBCONJUNTO

El conjunto A es subconjunto de B si y sólo si los elementos de A están contenidos en B. Su símbolo es ⊆ , su negado es ⊈

A⊆B≡(x∈B⇒x∈A)

Gráficamente:

Se lee: 

• A subconjunto de B
• A está contenido en B
• A esta incluido en B

NOTA:

• La relación entre elementos y conjuntos es de pertenencia ∈
• La relación entre conjuntos es de inclusión ⊆

CONJUNTOS IGUALES.- Es cuando A está incluido en B y viceversa

(A=B)↔[(A⊆B)^(B⊆A)]

CONJUNTOS POTENCIA.- Está formado por todos los subconjuntos posibles de ese conjunto. 

Cardinalidad del Conjunto Potencia

N(P(A)) = 2^N(A)

CONJUNTOS DISJUNTOS.- Son distintos sí, y sólo si no tienen elementos iguales.

CONJUNTOS INTERSECANTES.- Cuando hay elementos en común.

Más ejercicios de Conjuntos 

CUANTIFICADORES

Se pueden considerar tres tipos de expresiones: verdaderas, falsas y abiertas.

Las expresiones abiertas pueden ser verdaderas o falsas dependiendo del valor x

Para restringir o cuantificar la variable añadimos cuantificadores a estas expresiones, lo cual convierte en proposiciones y permitirán darle un valor de verdadero o falso.

CUANTIFICADOR UNIVERSAL.- Cualquier expresión de la forma: "para todo", "todo", "para cada", "cada". Se simboliza por medio de ∀

∀x, 2x+3x=5x

x=0          2(0)+3(0)=5(0)

x=1            2(1)+3(1)=5(1) ➡ 2+3=5 ➡ 5=5

x=2           2(2)+3(2)=5(2) ➡ 4+6=10 ➡10=10

CUANTIFICADOR EXISTENCIAL.- Cualquier expresión de la forma: "existe", "algún", "algunos", "por lo menos uno", "basta que uno", constituye en el lenguaje formal un cuantificador existencial y se simboliza por medio de ∃

∃x, x-3=10

Se lee "Existe al menos un número x, para el cual x-3=10"

x=13            13-3=10 ⇾ 10=10

OPERACIONES CON CONJUNTOS 

1. Unión 
2. Intersección
3. Diferencia
4. Diferencia Simétrica
5. Complemento 

UNIÓN DE CONJUNTOS.- Es el nuevo conjunto formado por los elementos que pertenecen a A o B o a ambos conjuntos

AUB={ x/(x∈A) V (x∈B)

Ejemplos:

A={a,b,c,d}                               AUB={a,b,c,d,e,f}

B={c,d,e,f}

Sean los conjuntos;

Representar  A U B en un diagrama de Venn.

Para poder resolver este ejercicio, como los conjuntos A y B están definidos por comprensión, primero es conviene escribir estos conjuntos por extensión, para poder ver todos sus elementos;

Y luego, representamos la unión en diagrama de Venn;

INTERSECCIÓN DE CONJUNTOS.- Es el nuevo conjunto formado por los elementos que pertenecen a A y a B, es decir, por lo elementos comunes a ambos conjuntos.

A∩B={x/(x∈A) ^ (x∈B)

Ejemplo:

A={a,b,c,d}                              A∩B={c,d}

B={c,d,e,f}

DIFERENCIA DE CONJUNTOS.- Es el conjunto formado por los elementos que pertenecen a A y que no pertenecen a B

A-B={x/x ∈ A ^ x ∉ B}

COMPLEMENTO DE UN CONJUNTO.- Es el conjunto de elementos U que no pertenecen a A.

A´ ={x/x ∈ A U ^ x A}

DIFERENCIA SIMÉTRICA DE CONJUNTOS.- Es el conjunto formado por los elementos que pertenecen a A o a B pero no pertenecen simultáneamente a ambos conjuntos.

AΔB={x/x ∈ A V x ∈ B ^ x ∈ A ∩ B}

PROBLEMAS DE CARDINALIDAD

En una celebración de graduación, las 30 estudiantes del curso debatían acerca de la bebida que debía servirse. Finalmente se optó por dos bebidas: cóctel de frutas sin alcohol y zumo de naranjas.Sabemos que…

-20 personas bebieron cóctel de frutas sin alcohol 
-10 personas bebieron zumo de naranjas
-8 no concurrieron

Lo que queremos saber, es ¿cuántas de las personas que concurrieron, se sirvieron de las dos bebidas?

Procedimiento de resolución

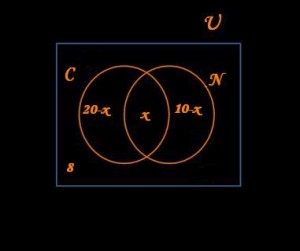
Te conviene disponer en esta ocasión, dos diagramas de Venn contenidos (como siempre) en un rectángulo “universo”. Al primero de los conjuntos le llamaremos C (por cóctel) y al segundo de ellos le llamaremos N (por naranja) y ambos se interceptan, es decir, habrá un espacio donde contener precisamente lo que es la incógnita de este problema, vale decir cuántas personas se sirvieron ambas bebidas. A este número de personas, por ser nuestra incógnita, le llamaremos “x”.

Es importante definir desde el principio cómo le llamaremos a la incógnita, pues habrá que restarla a los datos que nos da el problema, es decir a las 20 personas que sabemos certeramente que bebieron cóctel hay que restarle las que además bebieron zumo.

De este modo y con un razonamiento análogo para los que bebieron zumo (hay que restarle los que además bebieron cóctel), los sectores quedarían definidos de este modo:

•  20 – x = son las personas que bebieron cóctel pero no zumo
• x = son las personas que bebieron cóctel y zumo
• 10 – x = son las personas que bebieron zumo pero no cóctel

Por fuera de los diagramas de Venn, pero formando parte del “universo” hay que ubicar las 8  personas que no asistieron a la celebración.

Queda más claramente expresado, a través del siguiente diagrama de Venn:

Como siempre, el paso siguiente, es expresar todo lo antes razonado a través de una ecuación. En este caso, tenemos claro que la totalidad de personas antes señalada y analizada, suma un total de 30, por lo que esta sería la ecuación que debemos plantear y su correspondiente resolución:

(20 – x) + x + (10 – x) + 8 = 30
      20 – x + x + 10 – x + 8 = 30
                                   38 – x = 30
                                         – x = 30 – 38
                                         – x = – 8
                                            x = 8

La respuesta final a nuestro problema, es que son 8 las personas que bebieron ambas cosas, vale decir, cóctel de frutas sin alcohol y zumo de naranja.

Click para encontrar ejercicios de planteo

PROPIEDADES DE LAS OPERACIONES ENTRE CONJUNTOS 

Propiedad: Unión intersección Asociativa (A  B)  C = A  (B C) (A  B)  C = A  (B C) Conmutativa A  B = B  A A  B = B  A Idempotente A  A = A A  A =A Absorción A  (B  A) = A A  (A  B) = A Distributiva A  (B  C) = (A  B) (B  A) A  (B  C) = (A  B) (A  C) Neutralidad A  Ø = A A  U = A A   U = U A  Ø = Ø Complementación A  A l = U A   A l = Ø Ley de De Morgan (A  B) l = A l   B l (A  B) l = A l  B l Además se cumple:   (A l) l = A,       A  -  B  =  A  B l,      A -  (B  C) = (A - B)  (A - C),     A -  (B   C) = (A - B)  (A - C)

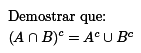RELACIÓN Y FUNCIÓN 

PARES ORDENADOS 

Un par ordenado es un conjunto de dos elementos, llamados componentes, en donde importa el orden de dichos componentes.

PRODUCTO CARTESIANO 

Es el conjunto de todos los pares ordenados cuyo primer componente es un elemento de A y el segundo componte es un elemento de B

A*B={(x,y)/x∈ A^ y ∈ B}

Ejemplo:

A={1,2,3,4}

B={a,b}

N(A*B)=[N(A)][N(B)]

N(A*B)=4*2=8

A*B={(1,a);(1,b);(2,a);(2,b);(3,a);(3,b);(4;a);(4,b)}

DOS CONJUNTOS RELACIONADOS 

En una relación binaria intervienen dos conjuntos, el primero se llama "conjunto de partida" y el segundo "conjunto de llegada"

REGLA DE CORRESPONDENCIA

Es una expresión que permite establecer una relación entre elementos de los conjuntos.

En toda relación existe una regla de correspondencia.

RELACIÓN

Una relación de A en B es el conjunto de pares ordenados (a,b) que cumplen con una condición o regla de correspondencia.

R={(a,b) ∈ A*B/a∈A, b∈B^R(a,b)}

DOMINIO DE LA RELACIÓN 

Es un subconjunto del conjunto de partida, formado por  los elementos que están relacionados.

RANGO DE LA RELACIÓN 

Es un subconjunto del conjunto de llegada, formado por los elementos que están relacionados.

EJERCICIO

Tenemos la relación r: B→A, r={(a,1),(a,*)}
Realizando su diagrama de flecha tenemos:

Dom r={a}

rg r={1,*}

FUNCIONES

Una relación será función solo si cumple 2 condiciones para ser función:

• Todo elemento del conjunto de partida x debe tener imagen Dom r=A
• Esta imagen debe ser única
• Toda función es relación pero no toda relación es función

FUNCIÓN INYECTIVA

Una función es inyectiva si a cada elemento del rango se le asocia con uno y solo un elemento.

FUNCIÓN SOBREYECTIVA

Cuando el rango y el codominio son iguales.

FUNCIÓN BIYECTIVA

Una función es biyectiva cuando es inyectiva y sobreyectiva a la vez.